Minimize the entropic Wasserstein distance

Minimize the entropic Wasserstein distance

minimize_entropic_W(
  Y,
  A = NULL,
  AV = NULL,
  P_D = NULL,
  muStart = NULL,
  maxIter = 100L,
  minIter = 50L,
  sinkhornIter = 100L,
  eps = 0.01,
  gammaStart = 0.05,
  p = 1,
  sinkhornTol = 1e-12,
  gradDescTol = 1e-12,
  fastSinkhorn = TRUE,
  pushforwardStart = FALSE,
  suppressOutput = FALSE,
  WThreshold = 0
)

Arguments

Y

numeric vector of observations

A

numeric vector of domain values where you expect most of the Y values to lie in

AV

numeric vector of domain values which you allow the functions in the space you minimize over to take

P_D

Jacobian of mu -> W_2(mu*D, pi_hat)

muStart

starting values for minimization

maxIter

maximum iteration number for gradient descent algorithm

minIter

minimum iteration number for gradient descent algorithm

sinkhornIter

maximum Sinkhorn iterations

eps

entropic regularization constant

gammaStart

starting gamma value for gradient descent algorithm. Only used in first descent step.

p

exponent of L_p norm

sinkhornTol

tolerance for stopping criterion in Sinkhorn algorithm

gradDescTol

tolerance for stopping criterion in gradient descent algorithm based on euclidian distance to last vector

fastSinkhorn

logical, controls whether to use the fast Sinkhorn algorithm

pushforwardStart

if TRUE, starts with nearest neighbour distribution to pi_hat instead of rep(1/n)

suppressOutput

suppress output messages?

WThreshold

tolerance for stopping criterion for gradient descent algorithm based on the Wasserstein distance

Examples

library(tidyverse)
#> ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.1 ──
#> ✔ ggplot2 3.3.5     ✔ purrr   0.3.4
#> ✔ tibble  3.1.6     ✔ dplyr   1.0.7
#> ✔ tidyr   1.1.4     ✔ stringr 1.4.0
#> ✔ readr   2.1.1     ✔ forcats 0.5.1
#> ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
#> ✖ dplyr::filter() masks stats::filter()
#> ✖ dplyr::lag()    masks stats::lag()
n <- 1000
x <- seq(0, 1, length.out = n)
m <- function(x) (2*(x- 0.5))^3
Y_no_error <-  m(x)
varepsilon <- rbernoulli_custom(n, a= -0.3, b= 0.3, p=0.5)
Y <- (Y_no_error + varepsilon) %>% sample(n)
dat <- tibble(x=x, Y=Y, Y_no_error = Y_no_error)
N <- round(sqrt(n))
A <- seq(-1.3, 1.3, length.out = N)
stepsize <- (A[2]-A[1]) / 2
A_V <-  A[which(-1 - stepsize <= A & A <= 1 + stepsize)]
p_ber <- function(x) pbernoulli_custom(x, a = -0.3, b = 0.3, p=0.5)
P <- matrix(rep(0, times = (N) * length(A_V)), nrow = N)
P[1, ] <- p_ber(A[2] - stepsize - A_V)
for (i in 2:(N-1)) {
    P[i,] <- p_ber(A[i + 1] - stepsize - A_V) - p_ber(A[i] - stepsize - A_V)
}
P[N, ] <- 1 - p_ber(A[N] - stepsize - A_V)

l <-
   minimize_entropic_W(Y = Y,
                       A = A,
                       AV = A_V,
                       P_D = P,
                       suppressOutput = FALSE)
#> Maximum number iterations reached (100).
mu_hat <- list()
mu_hat[["vals"]] <- l$vals
mu_hat[["probs"]] <- l$probs
g_hat <- measure_to_smooth_iso(mu_hat, n)
dat <- bind_cols(dat, g_hat = g_hat)
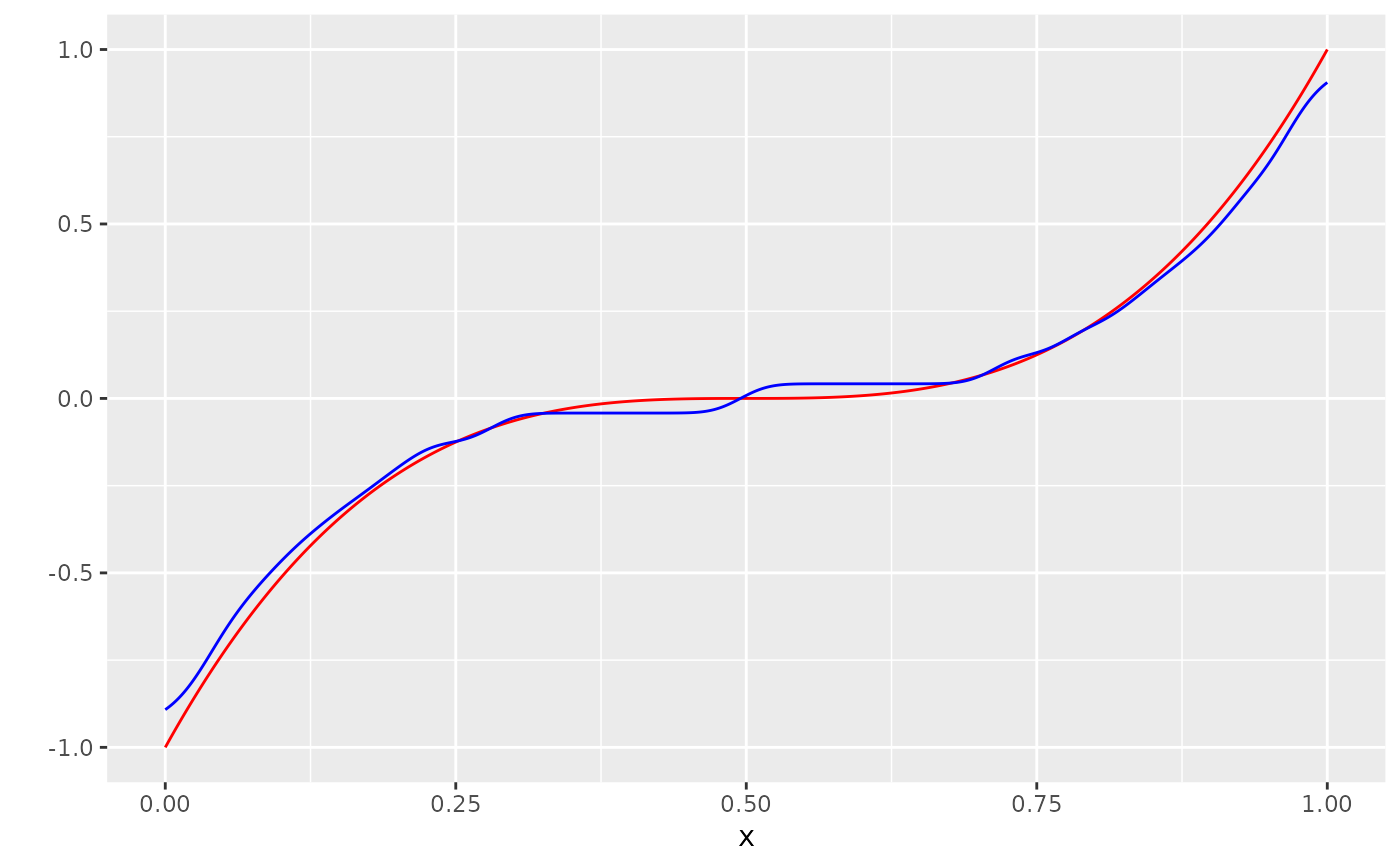
ggplot(dat, aes(x=x, y=Y_no_error)) +
  geom_line(col="red") +
  scale_y_continuous("") +
  geom_line(aes(y=g_hat), col="blue")